How to guage a units strengthMathematical balance metrics in competitive multiplayer gamesI have developped a general integral equation to calculate the cost of every unit for perfect balance. It includes a unit stat vector dependent function that describes the time dependency of relative hp during battles with every other unit (group). It can be applied on a game with any unit stat vectors. It's also possible to apply it on a game where you can build an infinite number of different units for example by choosing any real number as unit stats. If there's only a finite number of units integrals over unit stat vector space become sums. For ZK it will be nearly impossible to solve the equation analytically because of the high unit stat vector dimensionality. The time dependency of hp (and thus the whole equation) could be calculated by a simulation of the game itself where unit groups fight move against each other, though. But let's rather look at some simplified examples: For stat vectors (hp, dps) where any non-negative real numbers are possible I have calculated that strength (proportional to ideal cost) is hp*dps. Well, this was obvious, but getting this simple result from such a complicated formula is somewhat astonishing and supports its correctness. Here you can see a graph where units that win vs an arbitrary unit X are green: 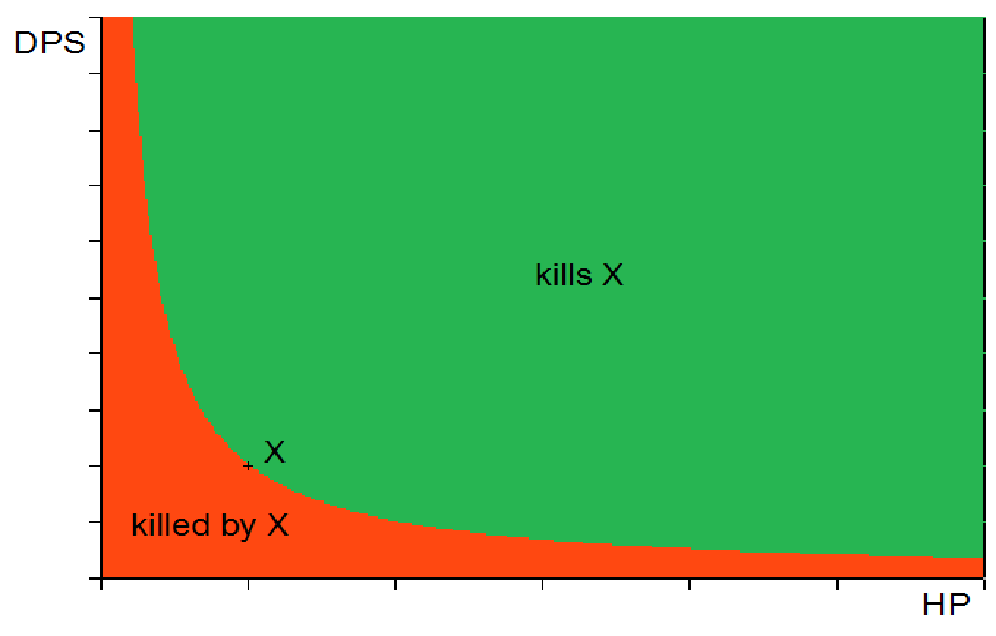 Now let's look at stat vectors (hp, dps, range, speed). Here we will get problems with infinities because some units are infinitely effective vs others which means they can kill any number of them without loosing any hp. That's the reason why it is said in ZK that only units of the same type can be balanced vs each other. But we can still calculate something between different types: If unit X has more range and speed than unit Y it can kill Y without any hp loss. Then X "outskirms" Y. If X has higher range, but lower speed than Y, Y's relative hp is reduced by (range_X - range_Y)/(speed_Y - speed_X)*dps_X/hp_Y while Y overcomes the range difference. If Y is already killed by this, X "outriots" Y. If Y survives the range difference but is then killed in the battle, X "riots" Y. If Y wins, Y "raids" X. Here you can see a graph of the relation of all units to an arbitrary unit X: 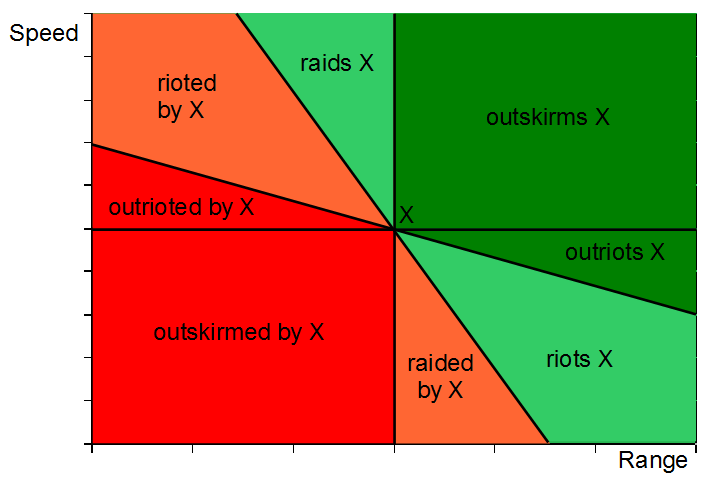 The gradient of the diagonals depends on (hp, dps).
+6 / -0
|
this balances a single unit vs. another single unit. The issue is that most encounters are in groups of different costs, so you actually have to balance a game for inherently imbalanced situations. A perfect balance for balanced situations may be terrible in practice if a numerically superior monospam force can beat another monospam force (of the same unit) with negligible losses.
+0 / -0
|
Exactly. That's why there is a simple generalization of my formula to unit groups. That's what I meant with: quote:
battles with every other unit (group) |
It doesn't change the form of the formula, it only integrates/summates over unit group spaces 1. to fight against and 2. wherein the unit itself fights instead of single unit spaces. The infinities of possible unit groups and unit group costs are already treated by the formula, so no problem here. It will only be even more complicated to calculate the relhp(time)-function and so on then. But in theory simulation of the game itself can still do it [Spoiler]until a limit because most computers have problems with calculating infinite iterations until their end. Using unit groups allows to consider repairing and eco buildings, too.
+0 / -0
|
Where is the "general integral equation"?
+3 / -0
|
I've never seen this type of thing successfully applied to ZK. One reason is that we have a lot of confusing integers (like alpha and cost). Another is all the physicsy stuff (turnrate etc...). Can you give us some example new unit prices?
+0 / -0
|
Yeah like how much should Mex cost?
+1 / -0
|
quote:
Can you give us some example new unit prices? |
quote:
For ZK it will be nearly impossible to solve the equation analytically |
Even aside from indirect combat utility (things which don't do damage can be useful: constructors, mex, placeholder, aspis, vulture, etc), i don't think that even when solved this equation would be very good at least for things that interest me (combat outcome prediction) because it seems to model combat as a continuous process where things like One Hit Kill don't happen. I would expect the equation to undervalue Duck vs Glaive, for example, because of Duck's DPS not being that much compensated by its health. However, it would be interesting to measure analytical (and other) combat models for their accuracy for combat prediction if there was a dataset of combats. Since that is useful in other ways too, maybe i'll try to figure out how to generate a reasonable dataset sometime autumnly, especially as replay archives are now accessible and scrapeable. Now, for the fun part. Not solving an equation analytically means solving it either by brute force, or by approximation, right? There was a series of interesting papers that achieved good combat outcome prediction accuracies by using machine learning. The one i found most intriguing was the one that assumed a simple lanchester's square law combat model with pairwise effective dps for each unit type, and machine-learned these pairwise DPS to make the model work. This was just a proof of concept for Starcraft, where armor modifiers are known and combat is fairly simple; for ZK, effective DPS could easily encode things like accuracy, leading, and maybe even AoE. (but not utility things like mentioned above: the lanchester model, even with pairwise dps, cannot model unit synergies and utilities) And again, applying that to ZK requires a dataset. What features should objects in such a dataset have?
+0 / -0
|
From what I've seen, Lanchester's laws are something that we would have to re-determine from first principles, rather than assuming them and basing our models on them, at least for raiders.
+0 / -0
|
quote:
For ZK it will be nearly impossible to solve the equation analytically |
For this to be useful you either have to provide insight or output some data. Non-analytic solutions are probably sufficient for data and insight. Anyone can come up with a completely intractable equation: ZK is a simultaneous execution turn based strategy game with a turn timer of 1/30th of a second. The orders you can issue in each of those 1/30th of a second increments are essentially finite due to engine enforced bandwidth limits. So to determine overall factory balance simply simulate a game with set factory plops and solve the game tree. `Just like' chess.
+0 / -0
|
I agree that without some tangible formula or result, whatever you found is not exactly useful knowledge. Saying "the cost effectiveness of a unit can be modeled around a fight function that takes unit stat vectors and outputs attrition" doesn't actually do anything to model unit relations, it just provides a formal framework for actual models. I mean, look, I came up with a general form of all major game engines. Even a large part of ZK fits that form!
+0 / -0
|
quote:
From what I've seen, Lanchester's laws are something that we would have to re-determine from first principles, rather than assuming them and basing our models on them, at least for raiders. |
Turns out i misremembered just how simple their model was. The actual paper uses somewhat more complex but still rather simple equations. Not exactly Lanchester, but not far from it either.
+0 / -0
|
What about 'steps' in effectiveness of units: Tank A deals 19 damage per shot. Tank B deals 20 damage per shot. Reload time is same. => Their DPS is almost the same. When the tanks fight an enemy with health=19 then both tanks kill it with one shot. When they fight an enemy with health=40 then Tank A requires an extra shot more than Tank B. zero-K makes heavy use of this in balance, tweaking health or damage by small values to ensure certain unit-combos take one more/less shot to kill each other.
+0 / -0
|
quote:
Tank A deals 19 damage per shot.
Tank B deals 20 damage per shot.
When the tanks fight an enemy with health=35 then both tanks kill it with one two shots. |
+0 / -0
|
|
|
I'm under the impression you're having more fun choosing function names than actually drawing useful conclusions :P
+0 / -0
|
Well, first of all I made a general theory and some simple results. Feel free to calculate further solutions if you can ;) You can't expect me to calculate the answer to life, the universe and everything in one day.
+0 / -0
|
Alright, so let me break down some of this math: The second centered formula (why didn't you number them???) says that if unit X costs 200 and unit Y costs 100, then X should have half its HP left the moment Y dies in a straight up battle. I don't see why that should "ideally" be true. In fact, raider/riot/skirmish triangles are easy counterexamples of this assumption. This also forces a very specific balance situation where bigger units always win in a battle of equal cost. Worse, this implies that all units are equally good against each other. That would probably the most boring game/unit selection I could imagine. Maybe this is an assumption/example by you, but it's not clearly marked as such and makes up a substantial amount of your document... [Spoiler]
I also fail to find a definition of ψ and ϕ, with the former being used both as a function, a function argument and a differential... Otherwise I'd try to wrap my head around the unit group idea (because that's an interesting topic), but I don't see how any of the standard meanings of ϕ would make sense here either.
+0 / -0
|
This kind of ideal balance you are referring to cannot and should not be true for every pair of units, specifically not if they are of different types as you said correctly. This first equation is only used as a motivation for the following integral equation, which says that this "ideal balance" should be true for a unit only on average. For example a raider will be more effective vs skirmishers and less effective vs riots. The integral calculates an average cost for that. The problem are infinite effectivities as described in my first post. But there are ways to solve that, for example only comparing same unit types or considering unit groups. chi and ψ are multisets which means functions that assign a number to every unit in the game to describe unit groups. For example a group of 2 Glaives and 1 Rocko would be described as ψ(Glaive)=2, ψ(Rocko)=1, ψ(everything else)=0, where units are unit stat vectors. ϕ depends on those functions and we integrate over those whole function spaces. [Spoiler]I added a description of ϕ as the unit group generalization of the superiority function s. Maybe it's better to remove the terms 1/chi(X) and integral_(Z in Omega\{X})chi(Z)f(Z)delta(Z)dZ in the last formula in "Generalization on unit groups".. Then it would be also much easier to calculate.
+0 / -0
|
Some more observations, starting from your integral before you set g(X)=1/f(X): For a fixed (f-independent) choice of g(X), your equations boil down to a simple linear system of equations. That should be easy enough to solve in a few example cases to demonstrate results. I'm too tired right now though (is lack of a solution for that system what you mean with your convergence problems?). I don't see why you choose g(X)=1/f(X). It seems downright arbitrary. Maybe I'm mistaken, but your resulting "simple" integral also yields weird/contradicting results: If s(X, Y)=0.5 (so s(Y, X)=2), then you conclude f(X)=0.5 and f(Y)=2, so f(Y)/f(X)=4 instead of 2 which the non-integral approach you started with suggests. If I'm not mistaken with that example, then there consequently must be a fallacy on the way through your example where you conclude f(X)~hp_X*dps_X, because it contradicts that. I can't find it right now though (although suddenly integrating over hp*dps instead of individual units is... confusing me? What if two units have identical values for that? Then you get a different result than your original integral...). Further, I think there's a dimension error in your first formula, because subtracting HP from DPS doesn't make sense in any case I can come up with. I totally missed the multiset meaning of ψ, despite it being very obvious. Oops! PS: It's "loser", not "looser" :P
+0 / -0
|
Okay, I have corrected the loser and hp/dps typing errors. You can also choose other g as long as it is decreasing enough in f(Y) so that it makes the integral converge. Otherwise if Omega is infinite the integral will be infinite, too. At first your example was shocking me, but now I think that the integral solves the problem. Even if X is half as strong as Y, the integral will only consider the battle between X and Y as part of an average. If Omega is finite or even only Omega={X,Y}, g=1 can be used to solve the problem, though. Even with finite Omega, the unit group space (natural numbers)^Omega is still infinite and may require other weighting functions then... For the hp*dps solution it would indeed be correct to integrate over dps and hp with two integrals. It can be seen that relhp's dependency in (dps_X,hp_X,dps_Y,hp_Y,t) can be reduced to (dps_X*hp_X,dps_Y*hp_Y,t). I just didn't write down every step of the calculation. In fact I calculated the integral in dependency of hp*dps already. But I have just recalculated it with two integrals and get the same result. quote:
I totally missed the multiset meaning of ψ, despite it being very obvious. Oops! |
Indeed very obvious as most forum readers will confirm :D ;)
+0 / -0
|

